
Tessellation is “a collection of shapes [tiles] that fit together without gaps or overlap to cover the infinite mathematical plane” (Fathauer, 2021). Most tilings are “periodic,” in the sense that the pattern repeats itself when “translated” (shifted without rotation). In the 1970s Roger Penrose described several sets of tiles that could cover the plane aperiodically. The search then began for the “einstein” (one stone) – a single tile that could cover the plane aperiodically. In March of 2023, Smith, Myers, Kaplan & Goodman-Strauss described a tile, commonly known as the “hat” that covered the plane aperiodically. However, to do so, this tile had to be occasionally turned over (to make its mirror image). Subsequently in May of 2023, the same authors reported another tile that could cover the plane aperiodically without any need for mirror images. This tile was called the “spectre.” This posting briefly reviews these recent developments in a style more visual than verbal.
Tiling a Surface
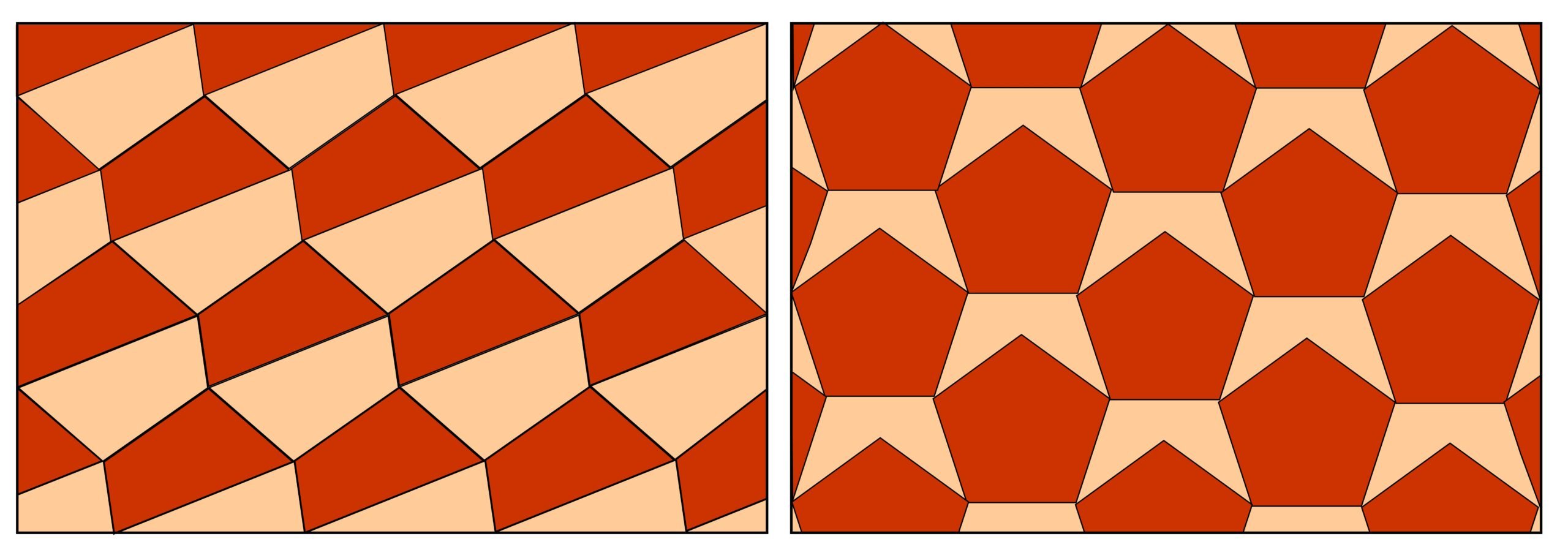
Many different patterns can tile a surface (Grünbaum & Shephard, 1987; Fathauer, 2021) Any triangle can completely cover a surface provide one allows the tiles to be rotated 180˚. Regular quadrilaterals and regular hexagons can cover the surface without the need for rotation. Irregular quadrilaterals can cover the surface if rotation is allowed (below left). Regular pentagons cannot cover the surface unless they are combined with tiles of a different shape (below right). Both illustrated tilings are periodic in the horizontal directions. The left pattern is also periodic along an axis at rotated a little clockwise from the vertical. The right pattern is also periodic in the vertical direction. This illustration (and all subsequent illustrations) can be viewed separately and in greater resolution by clicking on it.
Although regular pentagons cannot, some irregular pentagons can cover the surface. The following shows two pentagonal tilings – “Cairo” and “Floret.” In the latter, the pentagons are placed together in a hexagonal rosette.
Tiles of different shapes can be combined to form beautiful patterns. The following illustration shows a floor pattern from Pompeii with a striking trompe l’oeil effect.
Islamic culture avoids any representation of living forms since only the Divinity can create life. Islamic artists have therefore developed many different types of geometric ornamentation (Bonner, 2017). These patterns are tiled onto floors and ceilings, woven into rugs, carved through screens of wood or stone, and bound around beautiful books, The following are two intricate designs from the Alhambra taken from The Grammar of Ornament (1868) by Owen Carter Jones.
The Dutch artist Maurits Cornelis Escher (1898-1972) became fascinated by the Islamic designs that he saw in the Alhambra (Escher, 2008; Gelgi, 2010; Behrends, 2022). The following shows some tiling from the Alhambra together with a 1938 sketch by Escher (adapted from Wikipedia):
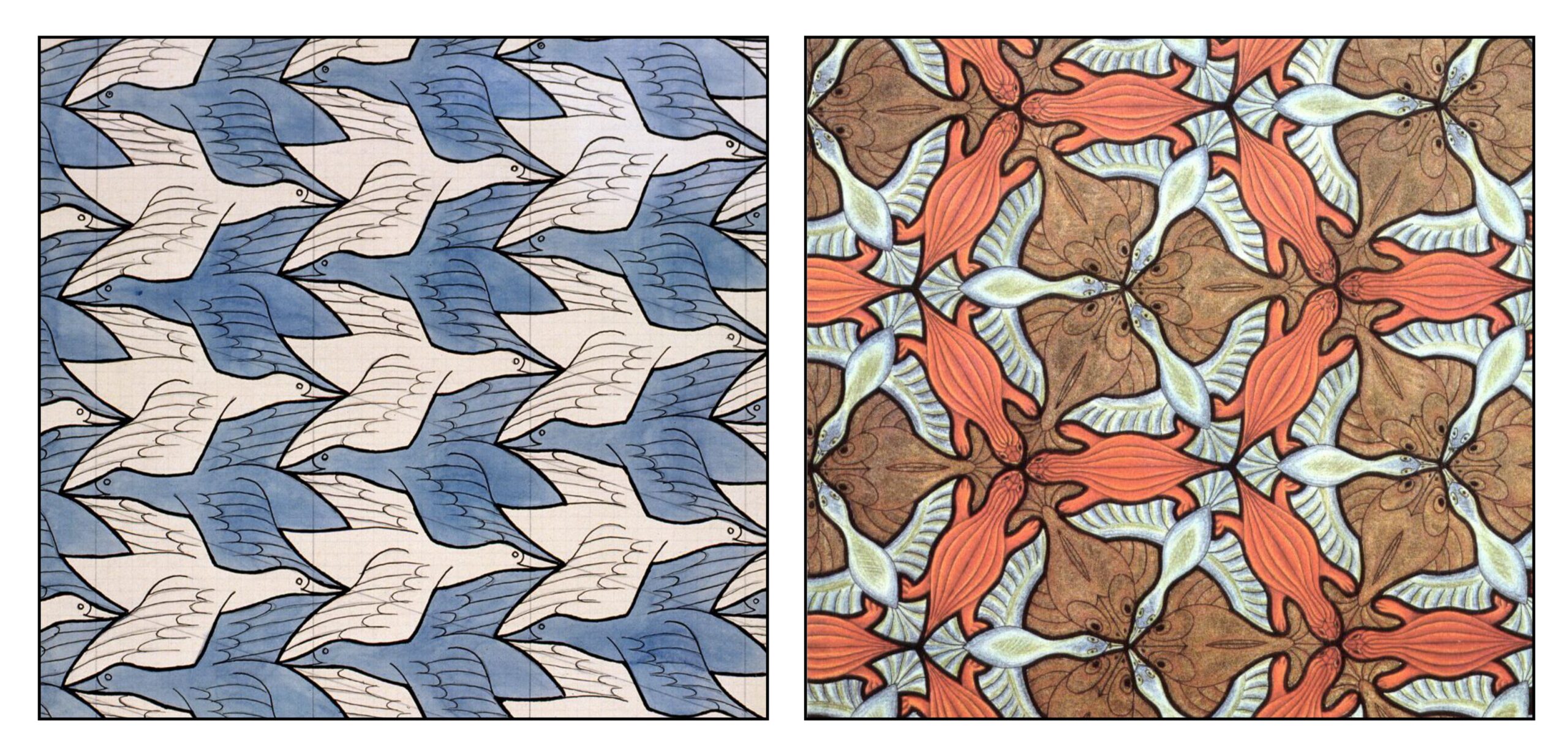
Escher evolved his own style of tessellation using representations of living things instead of geometric shapes. The following shows two representations of his work: a simple two-bird design from 1938 and a more complicated bird-fish-reptile design with three-fold symmetry from 1948.
Penrose Tilings
Later in his life Escher studied the problems of representing reality in two dimensions, and produced many illustrations of “impossible objects” such as The Waterfall (1961) in the illustration below. In the late 1950s, Roger Penrose, a mathematician whose work on black holes was to win him the Nobel Prize in 2020, and his father devised the “Penrose Triangle” which epitomizes the perceptual impossibilities portrayed Escher’s work
In the 1970s, Penrose became interested in the possibility of tiling the plane aperiodically (Penrose, 1974, Gardner, 1997). The following illustration shows some of his early ideas about tiling with pentagons (Penrose, 1978) together with a photographic portrait from about that time.
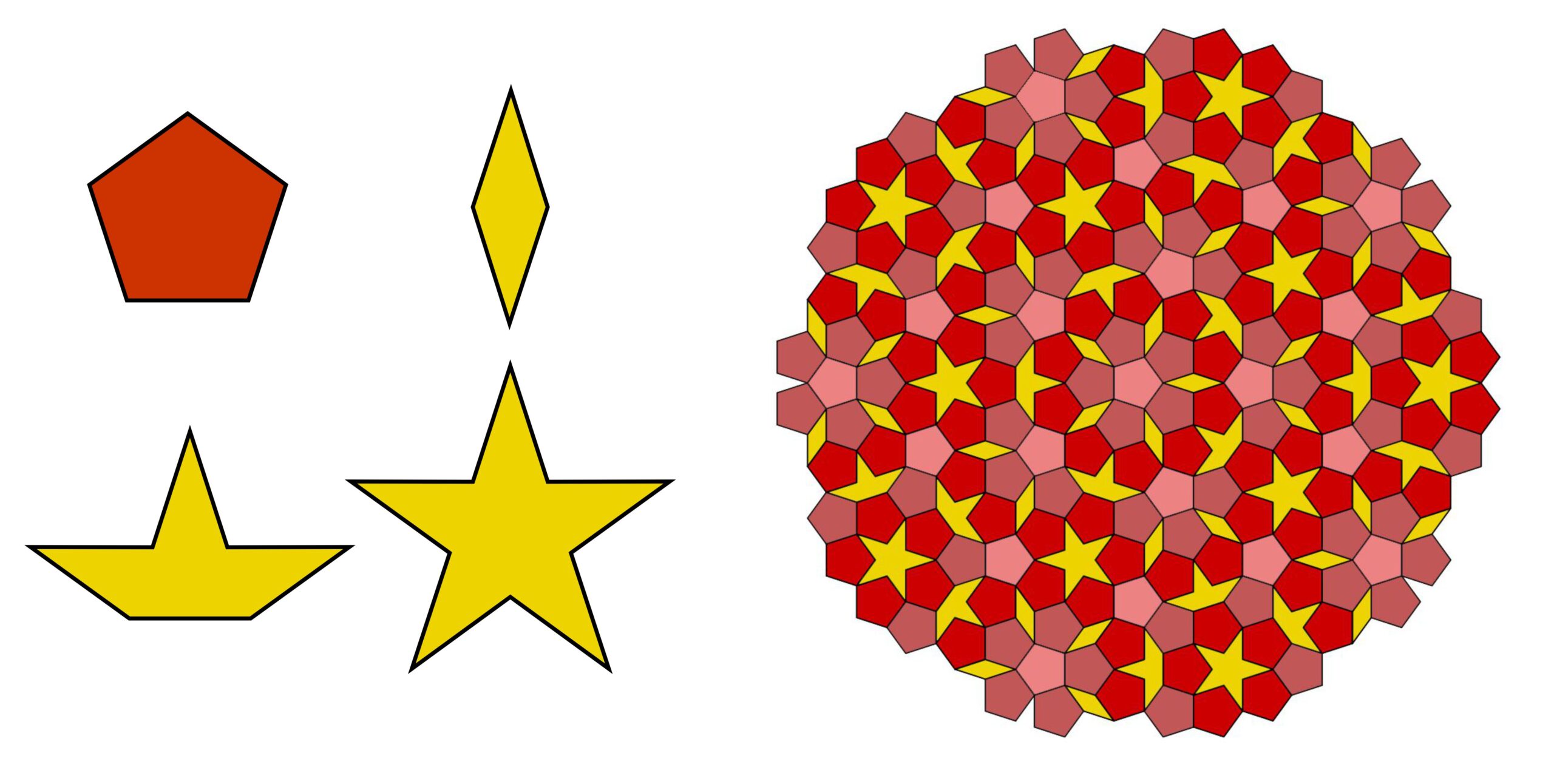
From these ideas he designed a set of tiles – a pentagon, a boat, a diamond and a pentagram – that could cover the plane aperiodically. However, in order for the tiling to succeed there had to be “matching rules” for what could adjoin the edges of the pentagon. These rules could be embodied by making the edges of the shapes notched or curved. In effect, this led to three kinds of pentagon. The following diagram, adapted from Wikipedia, shows the aperiodic pattern, with the three pentagons colored in different shades of red.
Penrose derived other patterns that tiled the plane aperiodically with only two shapes. Illustrated below is a tiling based on kites and dart shapes with the matching rules shown by the shading, and a tiling based on two rhombuses, with the matching rules shown in the colors. The tilings are aesthetically pleasing: like life, the shapes are the same but the pattern always changing.
Quasicrystals
Tilings explain how planes are covered; crystallography explains how spaces are filled. Only certain shapes can combine together to fill the space. According to classical physics, the crystalline structure of matter can show only 2-, 3-, 4- and 6-fold rotational symmetries on diffraction using x-ray or other radiation beams.
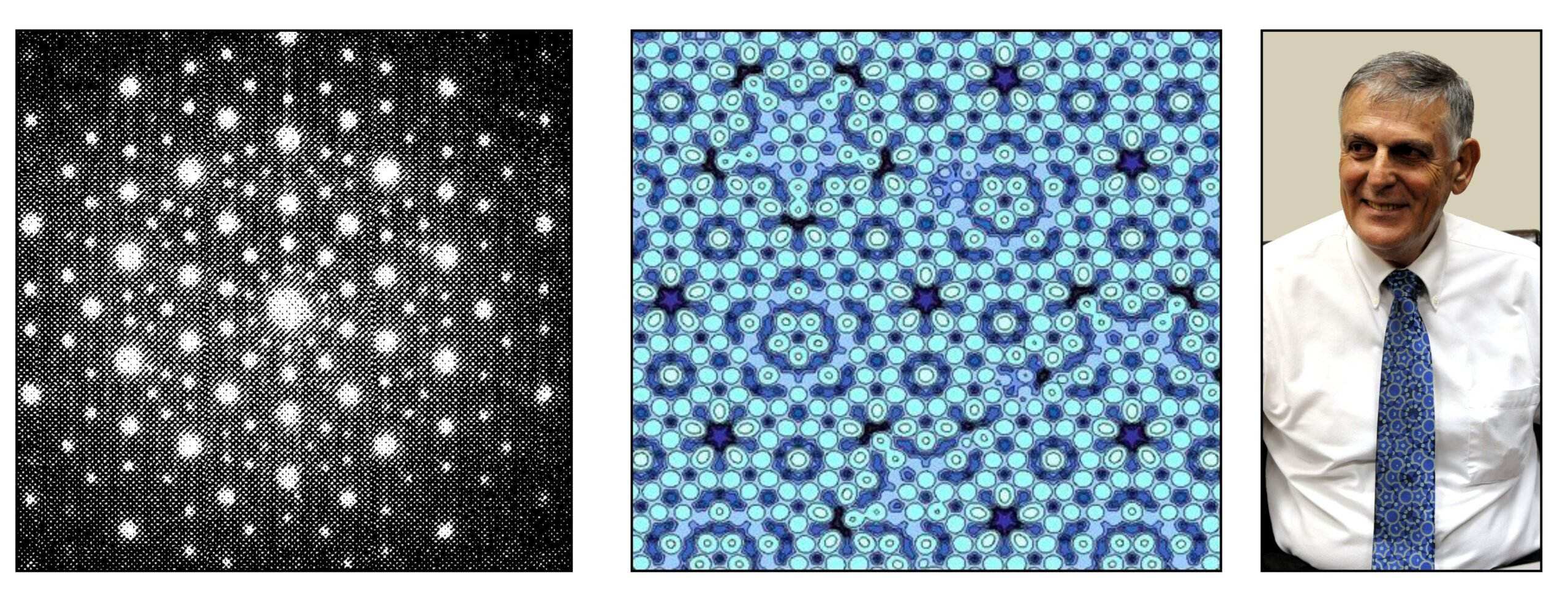
In 1984, Dan Shechtman and his colleagues reported a diffraction pattern of a metal alloy with ten-fold symmetry. From this initial finding came the study of quasicrystals (de Boissieu, 2012). Instead of tetrahedrons, cubes and octahedrons which can fit together to fill the space, decahedrons (ten-sided solids) and icosahedrons (twenty-sided solids) cannot fit together without other intercalating solids to fill the gaps. In effect these structures are the three-dimensional equivalents of Penrose’s pentagonal tilings.
Quasicrystalline structures have smooth hard surfaces. They are useful in non-stick cookware, non-corroding instruments, and broadband reflectors. Schechtman won the Nobel prize for his work in 2011. The illustration below shows one of the original diffractograms, the surface pattern of a quasicrystal, and a portrait of Schechtman wearing a tie showing the structure of another quasicrystal.
The Einstein Tile
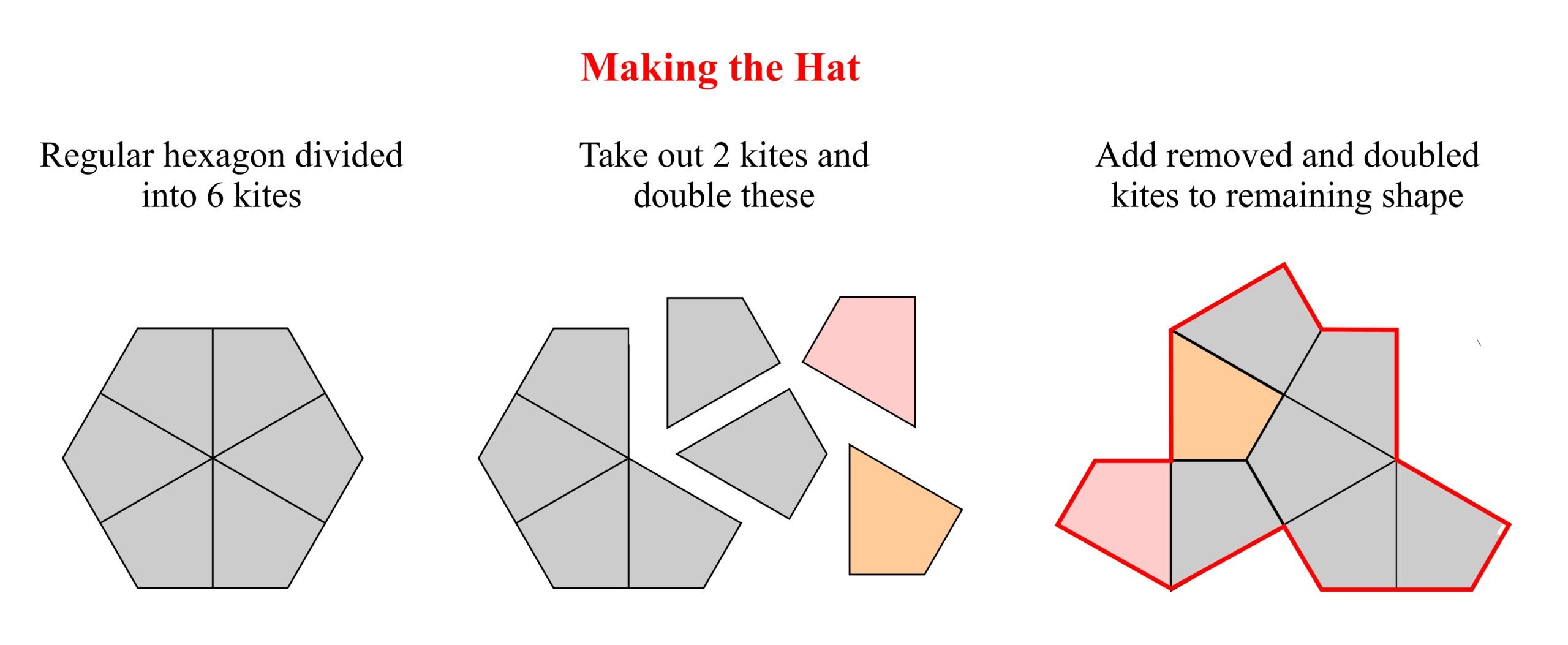
Once Penrose had shown that sets of shapes could cover the plane aperiodically, the question arose as to whether there a single tile – the ein Stein or “one stone” – could do so. In early 2023, David Smith, a retired print technician and amateur mathematician living in Yorkshire, discovered a shape – the “hat” – that apparently tiles the plane aperiodically. The structure of the hat is described in the following illustration:
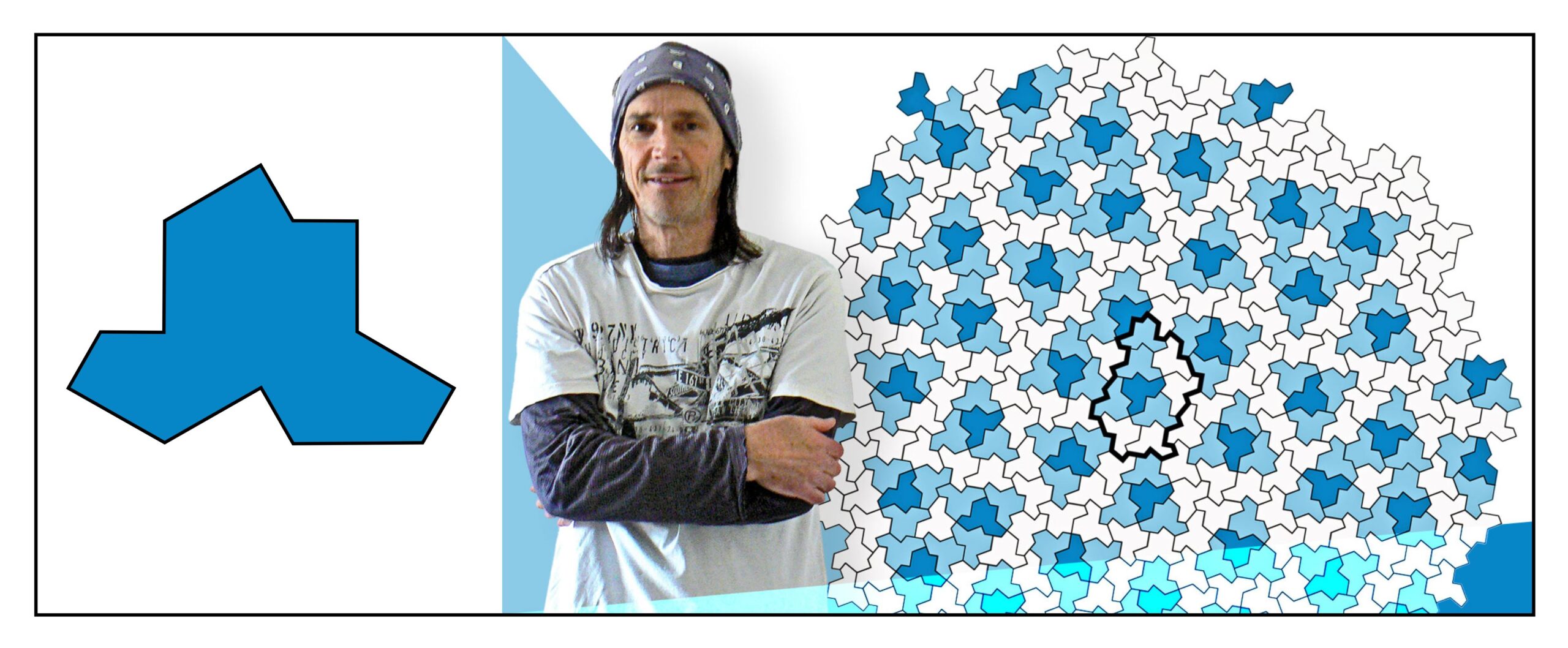
Smith contacted colleagues at the University of Waterloo in Canada, and they proved that this was indeed true (Smith et al, 2023a; Bischoff, 2023). The illustration below (derived from Whipple article in The Times) shows Smith together with his aperiodic tiling:
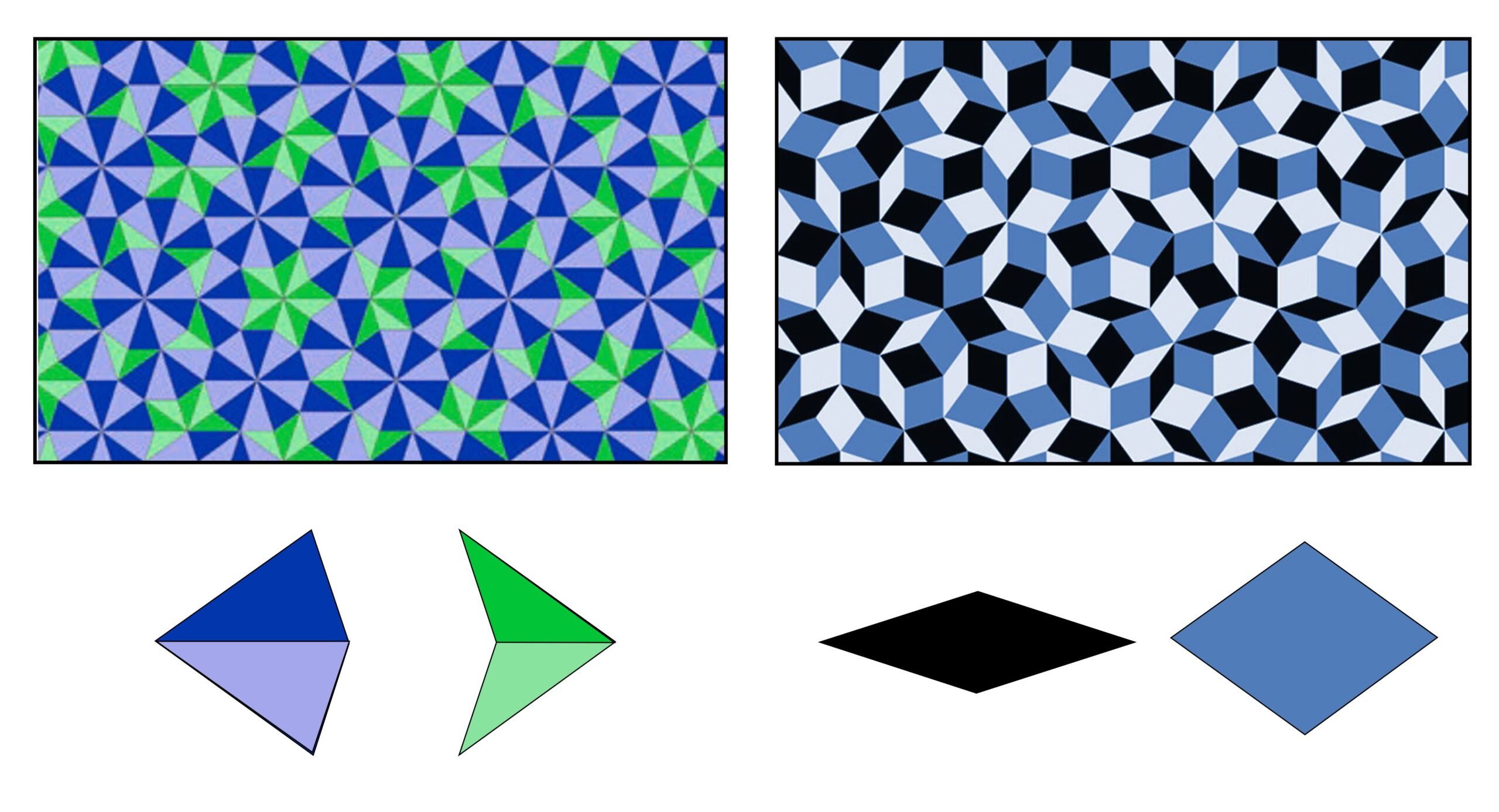
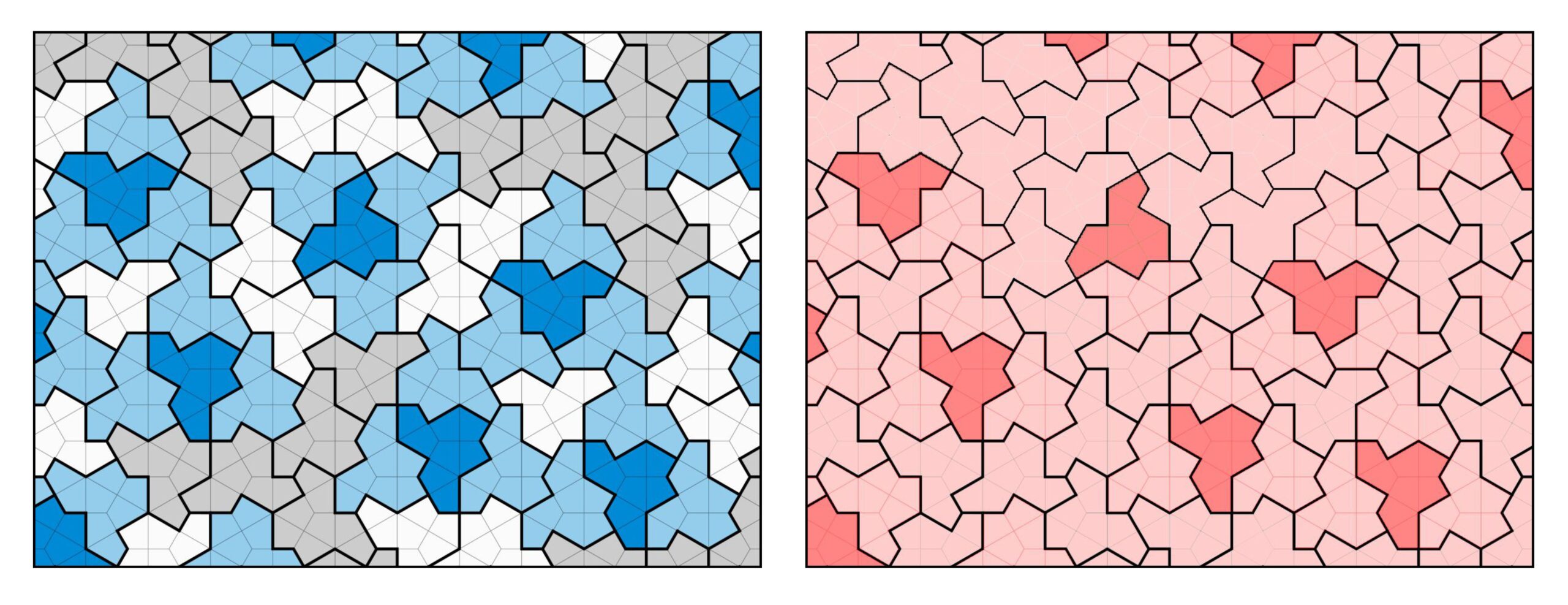
When the hat tiles the plane aperiodically, the pattern contains recognizable “metatiles.” These are shown in the illustration below left as the blue, white and grey combinations of hats. In order to tile the plane some of the hats have to mirror-inverted (equivalent to turning the hat over). This is shown in the illustration below right. In the real world where ceramic tiles are only finished on one side, this would require the manufacture of two separate tiles.
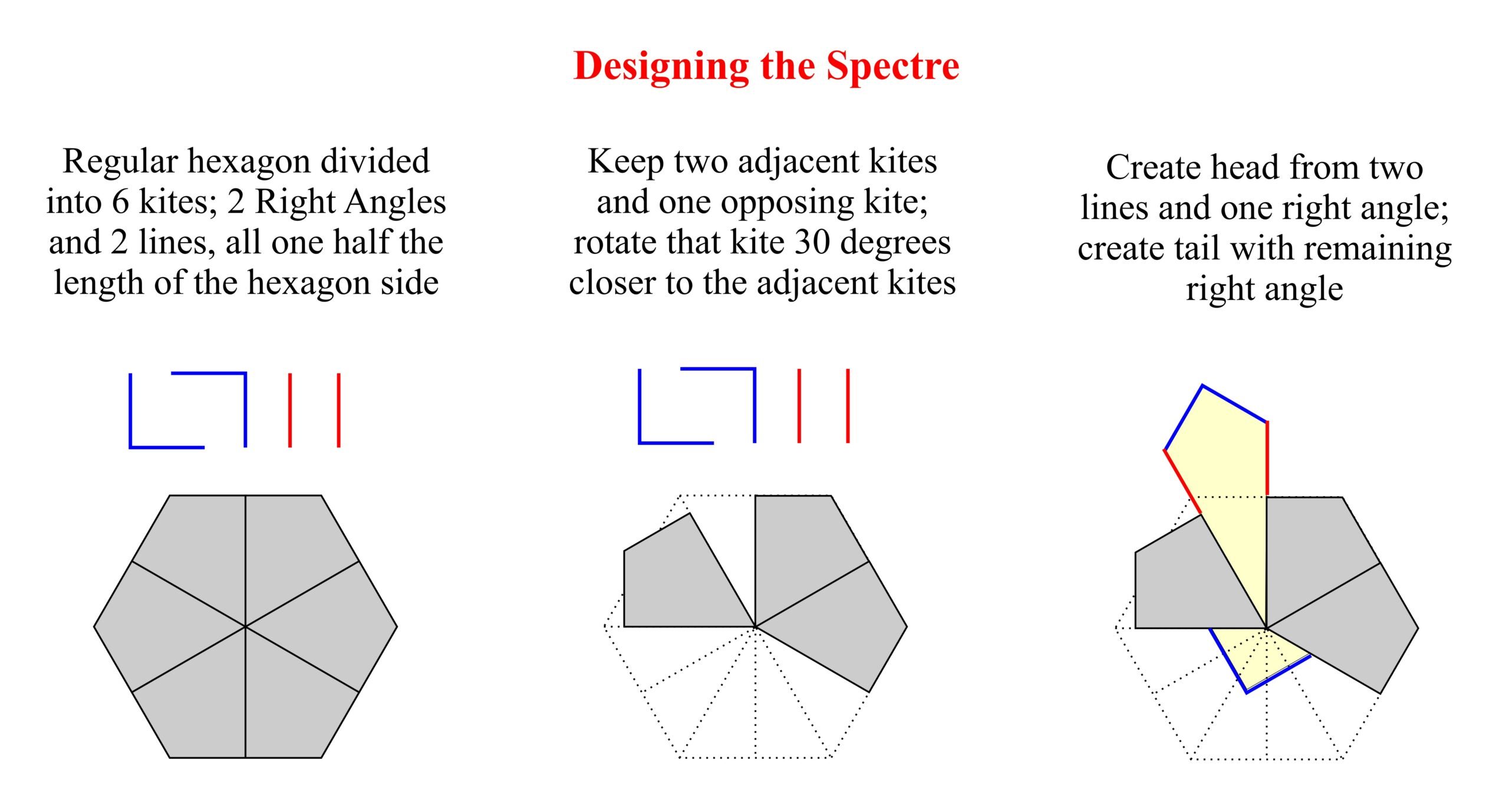
Soon after their initial report of an aperiodic monotile was published, Smith discovered another tile – the “spectre” – that could tile the plane aperiodically without any mirror-inversions (Smith et al, 2023b). The structure of the spectre tile is illustrated below:
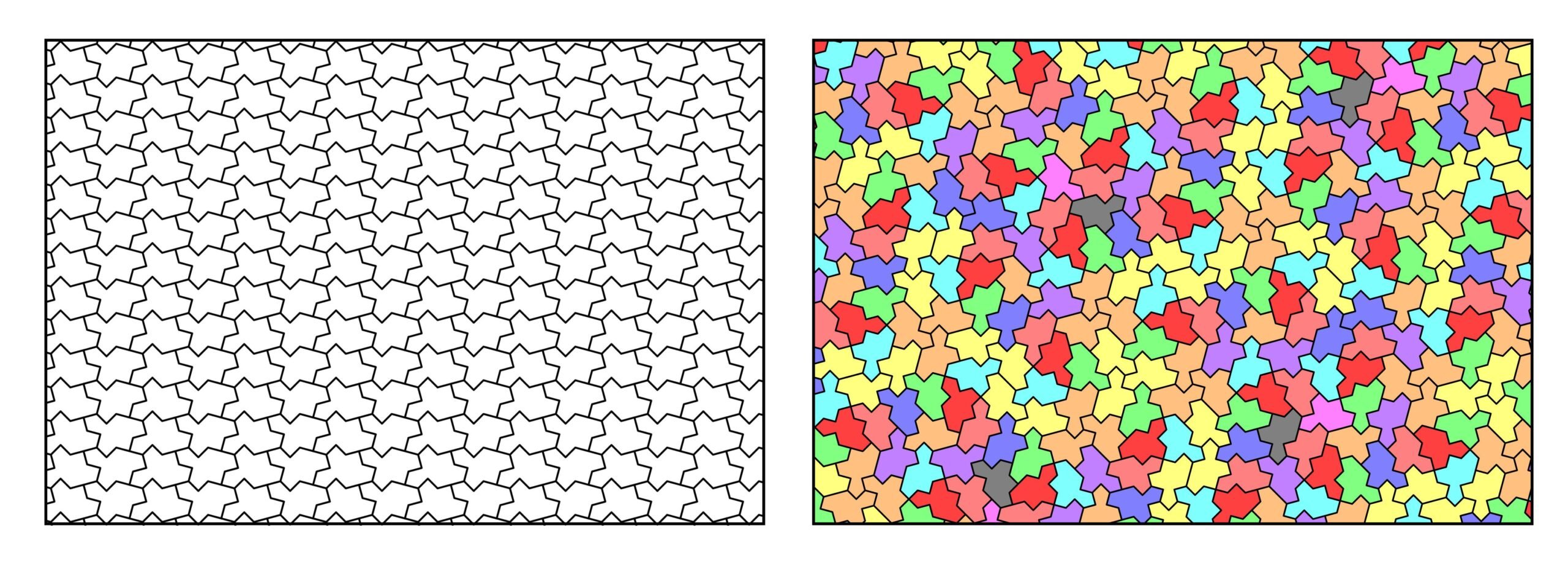
If mirror-inversions are allowed the spectre can tile the plane periodically (lower left); it is only if mirror inversions are forbidden and particular matching rules are in place, that aperiodic tiling is possible (lower right). Both illustrations are the work of Simon Tatham.
The following illustration is taken from the report by Smith and his colleagues. On the left the tiling shows the metatile structure of the tiling pattern and on the right the tiles have curved edges to enforce the matching rules.
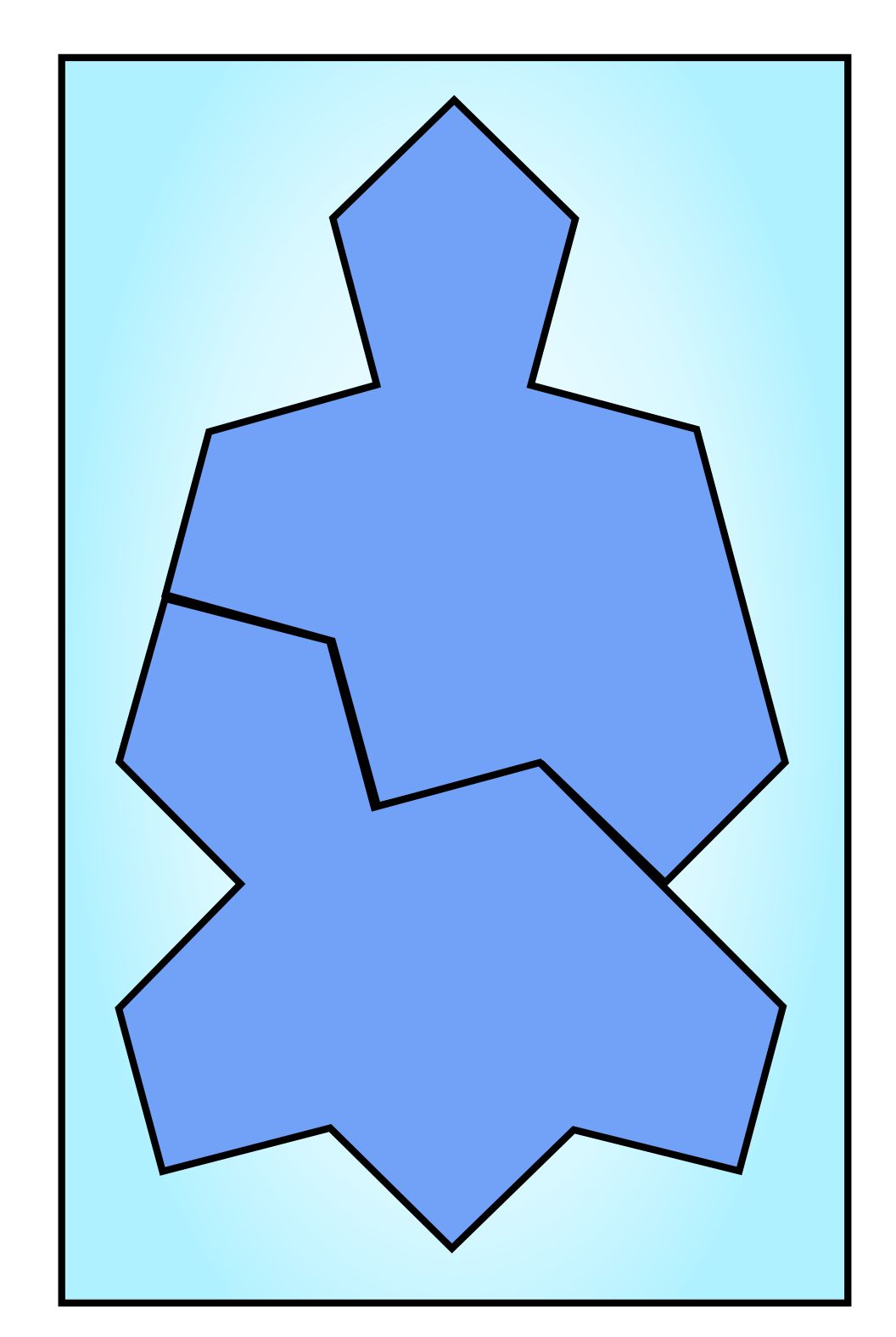
One of the repeating combinations that occurs in the spectre tiling is the “buddha” shape illustrated on the right. This combination is shaded in the illustration above, and by the red green combination in the illustration before that.
Envoi
Aperiodic patterns based on simple elements and uncomplicated rules are beautiful. They can represent a peaceful universe of myriad things.
References
Behrends, E. (2022). Tilings of the Plane: From Escher Via Möbius to Penrose. Springer.
Bischoff, M. (2023) Newfound mathematical Einstein shape creates a never repeating-pattern. cientific American, April 10, 1023.
Bonner, Jay. (2017). Islamic Geometric Patterns: Their Historical Development and Traditional Methods of Construction. Springer New York.
de Boissieu, M. (2012). Atomic structure of quasicrystals. Structural Chemistry, 23(4), 965–976.
Escher, M. C. (2008). The graphic work. Taschen.
Fathauer, R. W. (2021). Tessellations: mathematics, art, and recreation. CRC Press/Taylor & Francis Group.
Gardner, M. (1997). Penrose tiles to trapdoor ciphers: ̶ and the return of Dr. Matrix. Mathematical Association of America.
Gelgi, F. (2010). The influence of Islamic art on M. C. Escher. Foutain Magazine (July, 2010).
Grünbaum, B., & Shephard, G. C. (1987). Tilings and patterns. W.H. Freeman.
Penrose, R. (1974) The role of aesthetics in pure and applied mathematical research. Bulletin of the Institute of Mathematics and Its Applications, 10, 266-271.
Penrose, R. (1978). Pentaplexity. Eureka, 39, 16–22.
Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. (1984). Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Physical Review Letters, 53(20), 1951–1953.
Smith, D., Myers, J. S., Kaplan, C. S.; Goodman-Strauss, C. (2023a, March). An aperiodic monotile. arXiv:2303.10798
Smith, D., Myers, J. S., Kaplan, C. S.; Goodman-Strauss, C. (2023b, May). A chiral aperiodic monotile. arXiv:2305.17743
Whipple, T. (2023). Retired Yorkshireman solves elusive “Einstein tile” maths problem. The Times, April 3, 2023









Thank you Terry for another interesting installment. You mention the story of Quasicrystals and their discovery by Dan Shechtman, who is a colleague of mine at the Technion Faculty of Materials Engineering. The story of this discovery was an odyssey in its own right. Accepting this discovery was particularly difficult because the idea of ten-fold symmetry was vehemently rejected by crystallographers when Dan initially proposed it to explain his observations. So much so, that he was banished from the laboratory where he made these observations during a sabbatical, for “putting the laboratory to shame”. In addition, for years, Linos Pauling, who had received the Nobel Prize twice, used to say in his opening address to the Chemical Society that “there are no quasi-crystals, only quasi-scientists”. Dan did not take these insults personally, but, believing in his observations (made using electron microscopy, unlike classic crystallography which used X-Rays), persevered, and in collaborative work with Mathematicians and Physicists showed that his observations were theoretically sound. This Saga came to closure with the decision of the Nobel Committee to award him the 2011 Nobel Prize in Chemistry. In their decision they wrote that Dan Shechtman forced his peers to change their view on the nature of materials.
I thought I’d add this information because it provides lessons on the arduous course of progress in science and how solving seemingly purely theoretical problems like tiling and their associated aesthetics may impact our understanding of the very nature of matter.
Thank you, again, for this and all the other entries,
Hillel.
Many thanks, Hillel, for the background history to the discovery of quasicrystals. Science sometimes refuses to believe that which does not follow the currently accepted theories.