The concepts of determinism and freedom are nicely illustrated in a philosophical problem originally invented by William Newcomb, a California physicist. The philosopher Robert Nozick published an analysis of the problem in 1969, and since then it has been widely discussed (Nozick, 1969; Gardner, 1973, 1974, 2001; Drescher, 2005, Chapters 5 and 6; Mark in Malaysia, 2009, summarizes the issues on his webpage).
The basic problem is to decide how to act in the following situation. There are two boxes. The first contains $1000. You can see inside this box: the money is certainly there. The second contains either $1,000,000 or nothing. You cannot see inside this box. You can choose (i) to take both boxes or (ii) to refuse the first box and just take the second. A superior being predicts how you will choose and, before you do so, places in the second box either $1,000,000 if it predicts that you will refuse the first box, or nothing if it predicts that you will take both. The choice must be deliberate: it cannot be made on the basis of some random event such as a coin toss. How do you choose – one box or two?
Perhaps you need more information about the superior being who is predicting your choice? If you are a theist, the being can be likened to an omniscient God, who knows everything that will happen. The problem is then related to the concepts of predestination and free will. Christian believers have long sought to reconcile these two contradictory ideas. The one-box solution to problem suggests that you should renounce what you have for certain in the world to obtain the more valuable eternal salvation that can only be known by faith. Horne (1983) presents some other religious parallels.
If you are a scientist, the problem can be posed in an experimental context. Many other people have already tried the problem and the prediction of how they would choose was always correct. You should therefore infer that the prediction of your choice will also be correct.
If you are a neurophysiologist, the prediction can be made on the basis of a sophisticated brain scan that can tell which way you will choose before you make your choice (e.g. Bode et al., 2011, Haynes, 2011; Soon et al., 2011).
One box or two?
As Nozick remarked
To almost everyone it is perfectly clear and obvious what should be done. The difficulty is that these people seem to divide almost evenly on the problem, with large numbers thinking that the opposing half is just being silly. (p. 117).
Nozick, himself, believed that one should take both boxes (p. 135). He believed in the freedom of the individual and became famous for his 1974 book defending political libertarianism, Anarchy, State and Utopia. According to Gardner (1973), Newcomb argued for just taking the second box.
When Martin Gardner reviewed the problem for Scientific American (1974), readers of the journal who wrote in were 89:37 (approximately 3:2) in favor of just taking one box. In a review of what philosophers believe, Bourget and Chalmers (2014) found that of philosophers divided in the opposite way with 292 choosing two boxes to 198 only one. There were only low-level correlations with other beliefs: theists were more likely to choose one box, and those with a physical view of the mind more likely to choose two. Bar-Hillel and Margalit (1972) urge their reader to choose only the one box, and “join the millionaire’s club.” Schlesinger (1974) states that two boxes should be chosen, because voluntary choices are inherently unpredictable. Myself, I am a definite two-boxer.
Payoff Matrices and Decision Theory
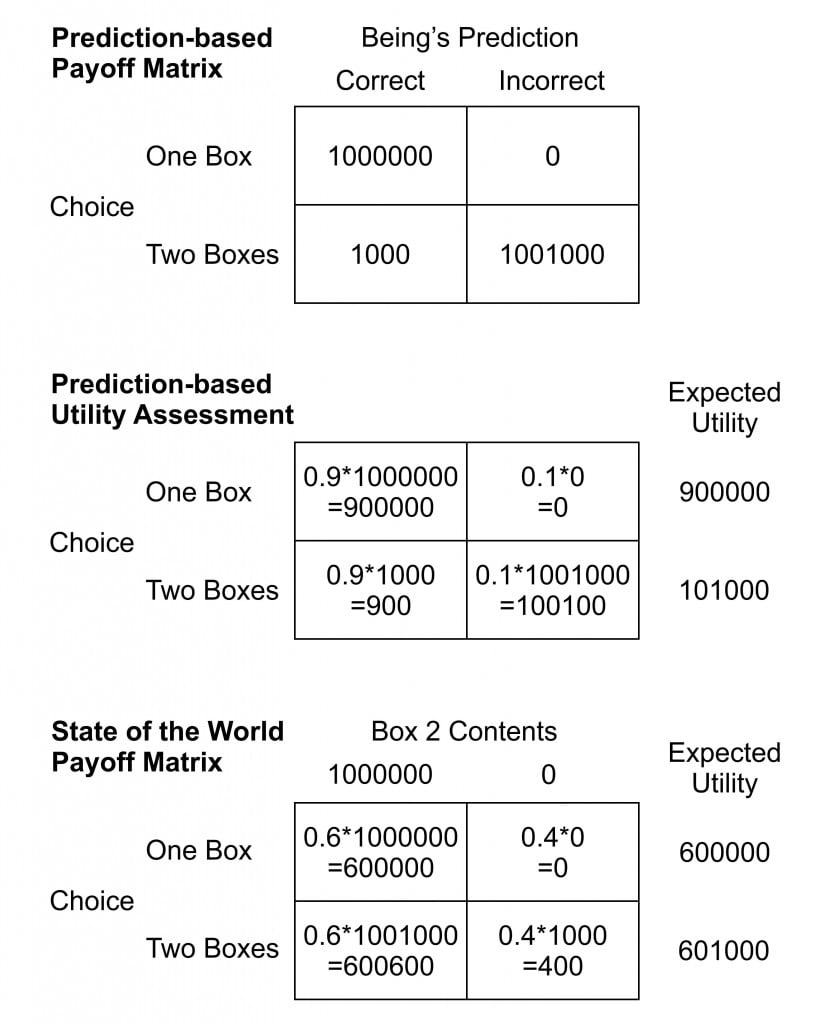 One approach to making a decision is to evaluate a payoff matrix. For the Newcomb problem the matrix is shown in the upper section of the figure on the right. Since we do not know what the future holds we have to consider the relative probabilities of what might happen. From the payoff matrix we can then assess the expected “utility” of a decision: how valuable the result is to the decider given the probabilities of each outcome.
One approach to making a decision is to evaluate a payoff matrix. For the Newcomb problem the matrix is shown in the upper section of the figure on the right. Since we do not know what the future holds we have to consider the relative probabilities of what might happen. From the payoff matrix we can then assess the expected “utility” of a decision: how valuable the result is to the decider given the probabilities of each outcome.
One way to assess the expected utility (middle section) is to estimate the accuracy of the superior being’s predictions For example we may guess that the superior being predicts our decision correctly 90% of the time. The expected utility of a decision is calculated by summing the payoffs for that decision with each payoff weighted by the probability of that outcome (lower section of the figure). One box is the better choice unless the chance of the superior being making a correct prediction becomes less than 50.05%. If the superior being acts by chance it might be worthwhile to take two boxes. We might also consider the possibility that the being is playing a joke or trying to outwit us, in which cases the prediction will be less than 50%
The expected utility is affected by other factors in addition to the relative probabilities of the possible outcomes. For example a decider may be “risk-averse,” preferring to have the certainty of the $1000 rather than risk the possibility (however low its probability) that there will be nothing in the second box: a bird in the hand is worth two in the bush. This can be factored into the assessment by applying a personal “utility function” that weights how valuable the decider considers each of the possible outcomes.
However, instead of being based on the predictions of the superior being, the payoff matrix can be set up according to the state of the world at the time of the decision (lower section of the illustration). In this case the first box contains $1000 and there is either $1000000 or $0 in the second box. The superior being has made a prediction and now it is up to you to decide. You do not know the probability of the second box being empty. The illustration uses a probability more likely to put money in that box. However, whatever this probability you always get $1000 more by choosing to take both boxes.
However, as Nozick points out, both these approaches do not really assess the relative utilities of the two decisions because the actions and the outcomes are not independent. In the basic statement of the problem the outcomes are necessarily correlated to the actions: your decision to take one box or two determines whether there is a million dollars in the second box or not.
An Ill-Posed Problem?
Newcomb’s problem might be explained by processes that we do not usually consider part of the real world. We could postulate “retrocausality:” the presence of the million dollars in the second box at a time after the decision somehow causes the decision, or my decision somehow causes the prediction that preceded it. However, this is not the world we understand. Causes precede their effects, not vice versa.
We could postulate “time travel:” the predictor may have travelled ahead to the time after the decision and therefore knows what it was (or will be). Again, the world we understand does not allow this possibility.
If we deny these imaginary processes, the problem then resolves to that of free will and determinism. Its insolubility may derive from the fact that these two assumptions are mutually contradictory. If I accept full determinism, I have no choice in the matter. My decision was determined when the world began.
With Earth’s first Clay They did the Last Man knead,
And there of the Last Harvest sow’d the Seed:
And the first Morning of Creation wrote
What the Last Dawn of Reckoning shall read.
(Rubaiyat of Omar Khayyam, translated by
Edward Fitzgerald, 1889, verse LXXIII)
I must therefore “choose” one box or two according to a sequence of cause and effect that is playing itself out according to rules I cannot alter. The future can be known to any intelligence that measures the current state of the universe and knows all the laws determining how it proceeds. The superior being can therefore predict my choice.
Why then do I spend time thinking about what would be the best thing for me to do? Should I not just act by instinct? Choose one box or two by intuition rather than by reason. Thinking about the problem is just a waste of time. Its only purpose may be to buttress my illusion that I am free to choose.
Free will assumes that the future is not fixed. We can act to change the course of events. No intelligence can predict with certainty what I shall do. Many of my actions can be predicted. Clearly, I am often a creature of habit. But not always. Between the prediction of how I shall choose and the moment of my actual choice, I can sometimes change my mind.
Bar-Hillel, M. & Margalit, A. (1972). Newcomb’s paradox revisited. British Journal of Philosophy of Science, 23, 295-304.
Bode, S., He, A. H., Soon, C. S., Trampel, R., Turner, R., & Haynes, J.-D. (2011). Tracking the unconscious generation of free decisions using ultra-high field fMRI. PLoS ONE 6(6): e21612.
Bourget, D., & Chalmers, D. J. (2014). What do philosophers believe? Philosophical Studies, 170, 465–500. The data from this study are available on the PhilPapers website. No correlations are listed for Newcomb’s problem. However one can obtain correlations with other variables by checking their listings (e.g. theism, physicalism).
Drescher, G. L. (2006). Good and real: Demystifying paradoxes from physics to ethics. Cambridge, Mass: MIT Press.
Gardner, M. (2001).The colossal book of mathematics: Classic puzzles, paradoxes, and problems. New York: Norton. Chapter 44 Newcomb’s paradox (pp 580-591). Based on original articles in Scientific American July 1973 (Free will revisited with a mind-bending prediction paradox by William Newcomb) and March 1974 (Reflections on Newcomb’s problem: a prediction and free will problem).
Haynes, J.D. (2011). Decoding and predicting intentions. Annals of the New York Academy of Sciences, 1224, 9-21.
Horne, J. R. (1983). Newcomb’s problem as a theistic problem. International Journal for Philosophy of Religion, 14, 217-223.
Nozick, R. (1969). Newcomb’s problem and two principles of choice. In N. Rescher(Ed.) Essays in Honor of Carl G. Hempel (pp. 114-146). Dordrecht: D. Reidel.
Nozick, R. (1974). Anarchy, state, and utopia. New York: Basic Books.
Schlesinger, G. (1974). The unpredictability of free choices. British Journal for the Philosophy of Science, 25, 209-221.
Soon, C. S., He, A. H., Bode, S., & Haynes, J.D. (2013). Predicting free choices for abstract intentions. Proceedings of the National Academy of Sciences USA, 110, 6217-6222.




Leave a Reply